Поможем улучшить онлайн-школу — без сложностей
Возьмём на себя самое сложное — осмысленную практику. Подключите нашу платформу как модуль заданий и разборов



Возьмём на себя самое сложное — осмысленную практику. Подключите нашу платформу как модуль заданий и разборов



Быстрый запуск обучения
Вы легко масштабируете курс: подключили — и сразу даёте ученикам полноценную учебную среду
Меньше рутины
Преподаватели тратят меньше времени на проверку шаблонных заданий — и больше на индивидуальные разборы.
Всё под рукой
Ученики не теряются между теорией и практикой — всё в одном интерфейсе, с прямой ссылкой на учебник.


обновить задачи

Более 50 000 задач по школьным и институским темам, а также авторские задачи
Огромная база задач
Все задачи структурированы: по предметам, классам, темам, уровню сложности и типу подготовки. Возможность быстрого перехода от задачи к теории
Генерация задач
На платформе есть возможность генерировать похожие задачи, при помощи ИИ для отработки темы
№ 155
Найдите значение выражения: $0{,}07 + 0{,}1001 : 1{,}43$
Решение №155: Для решения выражения $0,07 + \frac{0,1001}{1,43}$ выполним следующие шаги:
1. Запишем
выражение:
$$0,07 + \frac{0,1001}{1,43}$$
2. Выполним деление:
$$\frac{0,1001}{1,43} \approx
0,07$$
3. Сложим результаты:
$$0,07 + 0,07 = 0,14$$
Таким образом, значение выражения $0,07 +
\frac{0,1001}{1,43}$ равно $0,14$. Ответ: $0,14$
№ 265
Вычислить: $(\frac{3,75 + 2\frac{1}{2}}{2\frac{1}{2} - 1,875} - \frac{2\frac{3}{4} + 1,5}{2,75 - 1\frac{1}{2}}) \cdot \frac{10}{11}$
Решение №265: Для решения выражения $(\frac{3,75 + 2\frac{1}{2}}{2\frac{1}{2} - 1,875} -
\frac{2\frac{3}{4} + 1,5}{2,75 - 1\frac{1}{2}}) \cdot \frac{10}{11}$ выполним следующие шаги:
1.
Переведем смешанные числа в десятичные дроби:
$$2\frac{1}{2} = 2,5, \quad 2\frac{3}{4} = 2,75, \quad
1\frac{1}{2} = 1,5$$
2. Подставим десятичные дроби в выражение:
$$(\frac{3,75 + 2,5}{2,5 - 1,875} -
\frac{2,75 + 1,5}{2,75 - 1,5}) \cdot \frac{10}{11}$$
3. Выполним сложение и вычитание в числителях и
знаменателях дробей:
$$\frac{3,75 + 2,5}{2,5 - 1,875} = \frac{6,25}{0,625}; \quad \frac{2,75 +
1,5}{2,75 - 1,5} = \frac{4,25}{1,25}$$
4. Упростим дроби:
$$\frac{6,25}{0,625} = 10; \quad
\frac{4,25}{1,25} = 3,4$$
5. Выполним вычитание дробей:
$$10 - 3,4 = 6,6$$
6. Умножим результат на
$\frac{10}{11}$:
$$6,6 \cdot \frac{10}{11} = \frac{66}{11} \cdot \frac{10}{11} =
\frac{660}{121}$$
Таким образом, решение выражения есть $\frac{660}{121}$. Ответ: $\frac{660}{121}$
№ 863
В двух магазинах были одинаковые цены. В одном магазине их сначала понизили на 15%, а потом повысили на 10%, а в другом – сначала повысили на 10%, а потом понизили на 15%. В каком из магазинов выгоднее покупать товар?
Решение №863: Для решения задачи определим, в каком из магазинов выгоднее покупать товар, выполним
следующие шаги:
1. Пусть $P$ — начальная цена товара в обоих магазинах.
2. В первом магазине сначала
понижают цену на 15%, а затем повышают на 10%.
3. Вычислим цену после первого понижения на 15%:
$$P_1
= P - 0,15P = P(1 - 0,15) = 0,85P$$
4. Вычислим цену после последующего повышения на 10%:
$$P'_1 =
0,85P + 0,10 \cdot 0,85P = 0,85P(1 + 0,10) = 0,85P \cdot 1,10 = 0,935P$$
5. Во втором магазине сначала
повышают цену на 10%, а затем понижают на 15%.
6. Вычислим цену после первого повышения на 10%:
$$P_2
= P + 0,10P = P(1 + 0,10) = 1,10P$$
7. Вычислим цену после последующего понижения на 15%:
$$P'_2 =
1,10P - 0,15 \cdot 1,10P = 1,10P(1 - 0,15) = 1,10P \cdot 0,85 = 0,935P$$
8. Сравним итоговые цены в
обоих магазинах:
$$P'_1 = 0,935P \quad \text{и} \quad P'_2 = 0,935P$$
9. Поскольку $P'_1 =
P'_2$, цена товара в обоих магазинах после всех изменений оказывается одинаковой.
Таким образом, в обоих
магазинах выгодность покупки товара одинакова. Ответ: В обоих магазинах выгодность покупки товара одинакова.
Библиотека оцифрованных учебников
На нашей платформе огромная библиотека оцифрованных учебников. В подборке — проверенные учебники и источники с дополнительной информацией.
Также можем оцифровать ваши материалы
У вас есть распечатанные конспекты, старые задачники или методички?
Превратим их в удобные, структурированные цифровые форматы готовые к использованию на любом устройстве.
Идеально для преподавателей, репетиторов, авторов курсов и студентов, которые хотят систематизировать знания
и делиться ими в цифровом виде.
Напишите — обсудим детали и подберём оптимальное решение!


Варианты
прошлогодних ЕГЭ
Для помощи в подготовке учеников, на нашей платформе загружены варианты прошлогодних экзаменов!
ИИ методист
Мы разрабатываем базу видео с разбором интересных и трудных тем. Под каждым видео наш ИИ методист добавляет задачи, для отработки новых знаний
Тренировочные тесты по предметам
Наш сервис предлагает онлайн-тесты по математике и физике, помогая абитуриентам и школьникам проверить свои знания
Интерактивная онлайн-доска
Наша доска разработана действующим репетитором и выиграла грант Fasie.
На доске можно не только писать, но и вставлять интерактивные графики из Desmos и GeoGebra, подставлять
формулы в реальном времени.
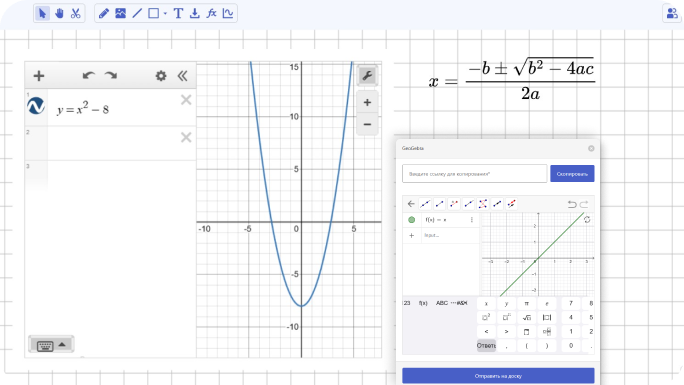
Веб-зазеркалье онлайн-доска
Мы разработали свою платформу для видеозвонков.
Видеозвонки, как индивидуальные, так и групповые, до 40 человек.
Без лимитов по времени и с чётким звуком без задержек.
Уроки, консультации, разбор задач — удобно и не уходя с платформы.




Подключение через LTI, iframe или API

Возможность кастомизации под ваш бренд (логотип, цвета, домен)

Гибкие тарифы для школ: от пилотного класса до полного внедрения

Поддержка на всех этапах — от тестового доступа до запуска
Хотите повысить вовлечённость и результаты
учеников —
без лишних усилий?
Оставьте заявку — и мы организуем демо-доступ, покажем, как платформа впишется в ваш курс, и обсудим условия сотрудничества
Оставить заявку

